ダルシー・ワイスバッハの式 は 次元解析 により得られた現象を記述する公式である。 流れの特性は配管に沿った位置とは無関係であり、重要な変量は配管単位長さあたりの水圧低下Δ p / L と体積流量である。 体積流量は流れの湿潤面積で割ることで断面平均流速 V に変換される。 配管が流体で満水の場合については湿潤面積は配管の断面積に等しい。 圧力の次元は単位体積あたりのエネルギーである。 ゆえに、2点間の圧力損失は (1/2)ρV2 の比となるはずであり、単位体積あたりの運動エネルギーに関する式に似て同じ次元となる。 さらに、単位長さあたりの圧力損失は一定であることから、圧力は2点間の配管長さ L に比例する。. ダルシー・ワイズバッハの式とハーゲン・ポアズイユの流れの式から、層流の場合の管摩擦係数は以下の式で与えられます。 この式から、層流の場合の管摩擦係数はレイノルズ数 Re のみに依存して決まることがわかります。 もっと知りたい 矩形管の流れ. 矩形管内の流れは円管に比べて複雑になりますが、管摩擦損失のみを考える場合には、矩形管と等価な円管を考えることによって、円管に関する式を用いることができます。 矩形管を等価な円管に置き換えたときの直径を 水力等価直径 、矩形管の周囲の長さのことを 濡れ縁長さ といいます。 ここでは例として、図3.46に示す矩形管を考えてみます。 図3.46 矩形管のサイズ.
管路 私の学習ノート

Images of ダルシー・ワイスバッハの式 JapaneseClass.jp
【配管の圧力損失とは?】計算方法と注意点を徹底解説│プラントエンジの樹
RX7のダルシーワイスバッハゆーやさんが投稿したカスタム事例|車のカスタム情報はCARTUNE
RX7のダルシーワイスバッハゆーやさんが投稿したカスタム事例|車のカスタム情報はCARTUNE

ファニングの式|ダルシーワイスバッハと比較|ムーディ線図の使い方 理系資格の教室

Images of ダルシー・ワイスバッハの式 JapaneseClass.jp

2018年度 分離化学工学 第11回 Speaker Deck

2018年度 分離化学工学 第11回 Speaker Deck

PPT Soil Mechanics I 土の力学 I PowerPoint Presentation ID6303279

H25 設問 Ⅲ3 分野1:土質および基礎

PPT 5 章 気液二相流 PowerPoint Presentation ID2339302

WO2016067559A1 管網解析装置、管網解析方法、及び、コンピュータ・プログラムが記録された記憶媒体 Google Patents
ダルシーワイスバッハゆーやさんがオーナーの車一覧|車のカスタム情報はCARTUNE

Images of ダルシー・ワイスバッハの式 JapaneseClass.jp

せん断応力を考慮するとベルヌーイの定理はどうなる? YouTube

【プラント設計の基礎】簡単な配管圧力損失の計算法を現役プラントエンジニアが解説! プラントエンジニアは語る

ダルシー・ワイスバッハの式

2.5.3 回路の諸損失 monozukurihitozukuri 日本のものづくり

【プラント設計の基礎】簡単な配管圧力損失の計算法を現役プラントエンジニアが解説! プラントエンジニアは語る
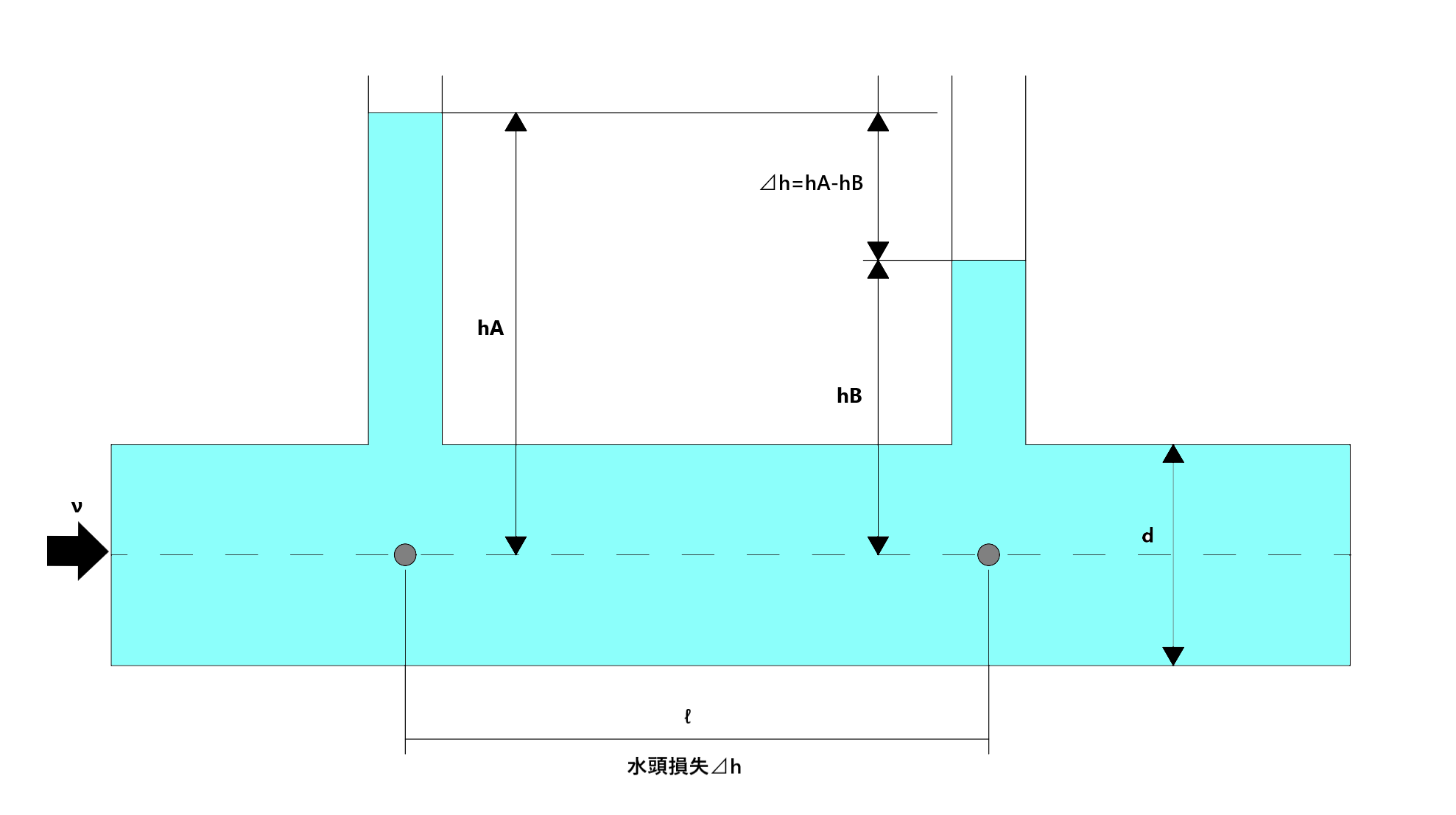
流体力学 において、 ダルシー・ワイスバッハの式 ( 英: Darcy-Weisbach Equation) は流れが十分に発達した円管内定常流の管壁による摩擦損失を与える式である。 この式は、配管に流れる流体と管壁の 摩擦 に起因する 損失水頭 、もしくは圧力損失を記述している。 この式は ヘンリー・ダルシー により開発され、1845年に ユリウス・ワイスバッハ により修正されているが、式の原型は プロニーの式 である。 式の名は ヘンリー・ダルシー 及び ユリウス・ワイスバッハ の名をとって名づけられた。 損失水頭式. 損失水頭 は次のように計算される。 円管にて満水の場合は、次のようになる。 ここで. hf: 摩擦による損失水頭 ( 国際単位系: m) L: 配管の長さ (m). ダルシー・ワイズバッハの式を変形した, は,動水勾配 I から断面平均流速を求める式と 考えることができる.しかし,摩擦損失係数 f が 既知であることが必要となる. [※摩擦損失係数の次元が無次元であることに 注意!



